Variable Timesteps and Holy Crap Math is Hard
Bullet hell shooters with intricate bullet patterns seem to rely on fixed timesteps to simplify the math. If you can ensure that every bullet is always handled consistently with the same timestep every frame regardless of actual framerate, you can pretty much guarantee that your pretty bullet pattern will deterministically look the same every time you run it on whatever hardware you run it on.
These games tend to handle a drop in framerate with a simple slowdown of gameplay. Sometimes this can be advantageous to the player, and even something desired by the designer themselves. And to make sure you aren’t cheating by artificially slowing down your game to a crawl, some measure of your average frame rate gets recorded next to your high score.
It’s a pretty simple approach, and it means that the bullet movement doesn’t have to be more accurate than one frame’s worth of linear movement, because it’s all consistent and everything is treated exactly the same frame-after frame. Basically, you don’t have to worry about your bullet pattern having uneven spacing or ugly breakages because some bullets launched in an earlier frame got a bigger change to their velocity because of the acceleration value than some bullets from some other frame.
An example of how some of these might run their iteration is:
- Check to see if we have any behavior change scheduled. This can be a change in any of: acceleration, speed, angle, angular velocity, or position. Angles can be offset from the direction to the target, and some values can be randomized (though it is discouraged).
- Add Acceleration to the current speed. There’s no need to multiply the acceleration by some time value, because the time value is fixed!
- Add the angular velocity to the current angle. Again, no timestep multiplication required.
- Add the vector [speed * cos(angle), speed * sin(angle)] to the current position.
- Check for collision with the enemy.
- Spawn any child bullets we’re scheduled to this frame.
- Destroy this bullet if we’re scheduled to this frame.
All time values for events (spawn, die, change behavior) can be done in frame counts instead of actual time values.
And None of That’s Gonna Fly in UE4
So UE4 does variable time steps. How on earth can we make variable time steps give the same level of consistency that we get from a simple movement in a fixed timestep simulation?
Let’s assume for the moment that I don’t care about floating point precision error, for the sake of sanity.
The angle, speed, angular velocity, and acceleration are all constant across some keyframe’s time. They aren’t interpolated as they would be if I had gone with the keyframe approach I was talking about before. In Danmakufu, they just change instantly at a scheduled frame number.
So I think we can come up with an equation that gives the velocity, in game plane space, at some time t, given those four starting values. I think I can do even better and replace speed with just a local space velocity vector, and acceleration with a local space acceleration.
(StartingVelocity, CurrentVelocity, Acceleration, and FinalVelocity are all vectors.)
CurrentVelocity = StartingVelocity + Acceleration * t
Angle = StartingAngle + AngularVelocity * t
FinalVelocity = [
cos(Angle) * CurrentVelocity[1] - sin(Angle) * CurrentVelocity[2],
sin(Angle) * CurrentVelocity[1] + cos(Angle) * CurrentVelocity[2]
];
This is the simple version that doesn’t clamp stuff to a maximum speed. The last line is really just a 2D rotation matrix multiplied directly by the velocity vector.
The complicated version takes the velocity vector, normalizes it (just divides it by its magnitude) and then multiplies it by the maximum speed. This is the version we want for after the velocity has hit maximum speed. Because you can only accelerate in one direction over the course of a keyframe, you can never go from over max speed to under max speed. Only from under max speed to over max speed. The exception being if you started off over max speed in one direction and accelerated back in the other direction. I’m eliminating that possibility by just clamping the velocity to the maximum speed for the actual value stored on the bullet state structure when it switches to a new keyframe.
All we have to do now is integrate FinalVelocity with respect to t.
Turns out that I have no idea how to do that! Yeah, I never actually made it through the integration part of calculus class. Derivatives were fine, but not integrals. Thankfully the class was split into two courses and I got to pass the first one.
My calculator kinda sucks
I figured I could just punch this whole thing into my TI-89 and mash the “integrate” (with respect to t) button. After thinking about it for a while, it spat back a really loooooong answer with many still un-integrated parts.
I was pretty disappointed! Mainly because the terrible UI on the calculator made it take forever to punch the stupid thing in.
Modes are BAD! (And the TI-89 makes you switch modes to go between text entry and anything-else entry!)
Time to learn something better? Finally?
I’ve been using that TI-89 for over a decade. I know the UI (well, the important parts) inside and out! How the heck am I going to learn something new? But even if the cell phone I carry around in my pocket has about a bajillion times the computing power of the oh-my-god-I-didn’t-know-they-sell-processors-this-weak-anymore TI-89.
So I’ve heard of Maple and Matlab. Looks like to even get a trial version of them you need to go through some silly process. To heck with that. I just want to solve one integral!
There’s got to be some open source Linuxy thing out there, right? What about GNU Octave? Well, that’s just a numerical solver. I want a symbolic solver. There is some symbols package for it, but I couldn't get it to do anything. (Wouldn’t even load?)
Hey, it’s just one problem, maybe Wolfram Alpha? Not a terribly conventient way to enter an equation so big. I mean, I guess I could try? Maybe I’ll dig around a little more first. I need a system where I can iterate on an idea. Something that takes a scripted input file and just outputs the integrated version of whatever equation I set up in there.
Dug around a little more. Found Maxima. Maxima is pretty sweet. At least my not-a-mathematician brain thinks so, anyway. After a brief learning curve, it looks like it can let me set up this crazy symbolic monstrosity, script the whole thing, plot it, integrate it, plot the integrated thing, and everything I ever used my TI-89 for. Awesome! So what does the script look like that I finally pieced together?
/* I couldn’t find a vector magnitude thingy in Maxima, so I just made my own. */
vecMag(x) := sqrt(x[1]*x[1]+x[2]*x[2]);
/* We just have to explicitly declare vectors to use them like vectors. */
StartingVelocity:[‘StartingVelocityX, 'StartingVelocityY];
Acceleration:['AccelerationX, 'AccelerationY];
Velocity:’('StartingVelocity + ’t * 'Acceleration);
/* This is what we’re trying to achieve. We need to split it into two
separate equations, though. I can’t integrate “clamp”. */
/*Speed:clamp(vecMag('Velocity), 0, 'MaxSpeed);*/
/* Non-maxspeed version. */
Speed:’(vecMag('Velocity));
/* Maxspeed version. */
/*Speed:'MaxSpeed;*/
NormalizedVelocity:’(Velocity / vecMag(Velocity));
VelocityAfterSpeed:’('NormalizedVelocity * 'Speed);
/* Angular velocity != 0 version. */
Angle:’('StartingAngle + 'AngularVelocity * ’t);
/* No angular velocity version. */
/*Angle:'StartingAngle;*/
/* Rotate the velocity vector by a rotation matrix. */
VelocityAtAngle:’(
[ cos('Angle) * VelocityAfterSpeed[1] - sin('Angle) * VelocityAfterSpeed[2],
sin('Angle) * VelocityAfterSpeed[1] + cos('Angle) * VelocityAfterSpeed[2] ]);
Result:integrate(ev(VelocityAtAngle, infeval), t);
ev(Result);
And what does it spit out?
(%o188) [(AccelerationX*((AngularVelocity*t+StartingAngle)
*sin(AngularVelocity*t+StartingAngle)
+cos(AngularVelocity*t+StartingAngle))
/AngularVelocity
+StartingVelocityX*sin(AngularVelocity*t+StartingAngle)
-AccelerationX*StartingAngle*sin(AngularVelocity*t+StartingAngle)
/AngularVelocity)
/AngularVelocity
-(AccelerationY*sin(AngularVelocity*t+StartingAngle)
+(-AccelerationY*(AngularVelocity*t+StartingAngle)
-AngularVelocity*StartingVelocityY+AccelerationY*StartingAngle)
*cos(AngularVelocity*t+StartingAngle))
/AngularVelocity^2,
(AccelerationY*((AngularVelocity*t+StartingAngle)
*sin(AngularVelocity*t+StartingAngle)
+cos(AngularVelocity*t+StartingAngle))
/AngularVelocity
+StartingVelocityY*sin(AngularVelocity*t+StartingAngle)
-AccelerationY*StartingAngle*sin(AngularVelocity*t+StartingAngle)
/AngularVelocity)
/AngularVelocity
+(AccelerationX*sin(AngularVelocity*t+StartingAngle)
+(-AccelerationX*(AngularVelocity*t+StartingAngle)
-AngularVelocity*StartingVelocityX+AccelerationX*StartingAngle)
*cos(AngularVelocity*t+StartingAngle))
/AngularVelocity^2]
Err... Okay. Well, I can deal with that. This is good, though. I don't know integration very well, and I sure as heck don’t know what in this corresponds to the thing I fed into it, but it works! And if I need to add some functionality to the bullet integration in the future, I can just go back to my script and modify the velocity equation.
Also, there are so many redundant terms in there that the optimizer on the compiler does a pretty good job of sorting it out.
I was pretty surprised by the fact that this version of the equation seems to be undefined for AngularVelocity=0. The integrated version has it in the denominator pretty much everywhere. So that’s why there’s a commented-out version that drops the angular velocity, and we just use that instead if we have to. It spits out a very different result:
(%o223) [cos(StartingAngle)*(AccelerationX*t^2/2+StartingVelocityX*t)
-sin(StartingAngle)*(AccelerationY*t^2/2+StartingVelocityY*t),
cos(StartingAngle)*(AccelerationY*t^2/2+StartingVelocityY*t)
+sin(StartingAngle)*(AccelerationX*t^2/2+StartingVelocityX*t)]
As expected, it’s just the velocity integration pointed in the angle’s direction.
Here’s what it looks like when we plot that position for some time t with some acceleration and angular velocity:
{% include article_image.md img="danmaku_ue4_maxima1.png" %}
(After plugging in actual values instead of variables, the equation got simplified.)
So now we can pretty much determine whatever the bullet’s position is for any time with just this one equation.
The MaxSpeed Monkey Wrench
So here’s what happens when you use the “MaxSpeed” version of the equation and tell Maxima to integrate it:
(%o874) [MaxSpeed*'integrate(t*cos(AngularVelocity*t+StartingAngle)/abs(t),t),
MaxSpeed*'integrate(t*sin(AngularVelocity*t+StartingAngle)/abs(t),t)]
It doesn’t even know what the heck to do with it.
In the end I opted for a much simpler but less accurate approach. I’ll just have acceleration zero out when it reaches max speed. This has a flaw, but I don’t think it’ll be a serious hindrance to authoring content.
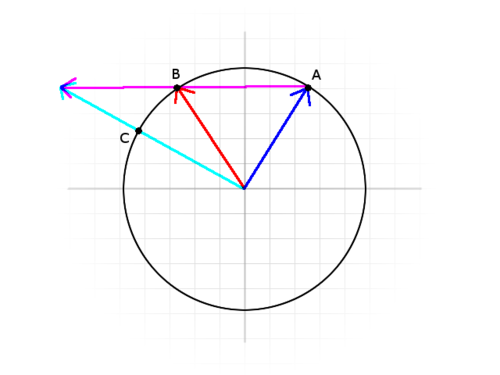
This is the flaw...
In this diagram, the blue line is the velocity vector from the last keyframe frame. Magenta is the acceleration vector. The radius of the circle is the maximum speed, so the velocity vector will hit the edge of the circle and stop accelerating.
If we zero out the acceleration when we hit another edge of the circle (magnitude of velocity is >= max speed), then we’ll start at point A, travel to point B, and then stop. If we didn’t clamp the velocity at all, the velocity vector might at some point look like the cyan arrow. Clamping the cyan line to max speed would get you point C. The problem is that, even though the speed isn’t changing, the direction is still changing as a result of acceleration. If you accelerate long enough, the velocity direction would even appear to approach the direction of the acceleration vector itself (clamped).
But I couldn’t integrate the equation for max speed correctly, so I’ll just do the dumb way that stops at B. I only have this problem at all because I allowed 2D vectors for the local space velocity and acceleration instead of a 1D speed and acceleration that just went down one axis. If it’s used like a 1D speed (just velocity and acceleration on a single axis) this issue evaporates entirely. That’s why I’m not worried about it.
Stuff
So I think I’ve proven here that I’m not really that great at calculus. So if anyone out there wants to tell me that I’m doing this all wrong and there’s a way easier way, I’d like to hear it!
(Unless it involves a fixed timestep or anything to do with bezier curves.)
In the meantime, I’m going forward with this.
Note: This article originally appeared on my Tumblr and was reposted here in 2019.